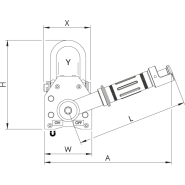
Quel est le principe de fonctionnement d’un aimant de levage ?
Fonctionnement des aimants de levage permanents

Fonctionnement des électroaimants de levage

Fonctionnement des aimants électro permanents

Quelles sont les exigences de sécurité et de conformité pour un aimant de levage ?
- Pour de nombreuses applications, un coefficient de sécurité standard de 3:1 est souvent utilisé. Cela signifie que la capacité de levage maximale (Capacité Maximale Utile - CMU) de l'aimant est trois fois supérieure à la charge maximale prévue. Par exemple, si la charge maximale prévue est de 1000 kg, l'aimant aurait une CMU d'au moins 3000 kg.
- Dans certaines applications ou industries, un coefficient de sécurité de 4:1 ou même 5:1 peut être recommandé. Ce coefficient est crucial pour pallier les erreurs de calcul de la force d'aimantation réelle et les effets dynamiques de l'appareil de levage.
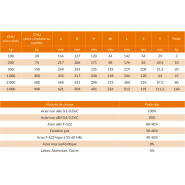
Normes légales et caractéristiques
Conditions d’intégration dans une installation industrielle
Dans une ligne de production, un aimant de levage peut être associé à des éléments supplémentaires :
- plaque de montage,
- anneaux de levage,
- tiroir, trappe, porte, ouvrants,
- tablette coulissante,
- support de fixation,
- intégration dans un rack 19 pouces,
- vérification d’un joint d’étanchéité lors de l’assemblage.
La conception mécanique, la modélisation 3D, l’analyse de RDM, et l’établissement d’un cahier des charges assurent une installation adaptée au poste de manutention.

Comment évaluer la charge maximale d’un aimant de levage ?
Avant d’utiliser un aimant de levage permanent, il est nécessaire de déterminer la force d’aimantation qu’il peut réellement exercer. Ce calcul permet d’identifier la charge maximale qu’il pourra lever en sécurité. Il est également utile lors de l’achat d’un aimant, car la performance réelle dépend de plusieurs paramètres :
- l’état de surface de la pièce,
- la composition du matériau (présence ou non de métaux non ferreux),
- l’épaisseur de la pièce,
- l’existence éventuelle d’un entrefer entre l’aimant et la surface.
Plus la surface de contact est irrégulière ou réduite, plus la force d’adhérence diminue. La matière de la pièce influe directement sur la puissance magnétique. Il est indispensable que le poids de la charge à lever reste inférieur au résultat obtenu pour éviter un décrochage.
Méthode de calcul de la force d’aimantation
La force d’adhérence se calcule à partir de la capacité nominale de l’aimant, multipliée par plusieurs coefficients liés aux caractéristiques de la pièce :
Force d’aimantation = Capacité de charge × T × S × M × G
- T : coefficient lié à l’épaisseur de la pièce
- S : coefficient associé à l’état de surface
- M : coefficient correspondant au type d’acier
- G : coefficient lié à l’entrefer
Pour les pièces cylindriques, la force obtenue doit être divisée par deux. Des abaques sont fournis pour déterminer les coefficients en fonction de la situation (épaisseur, entrefer…).
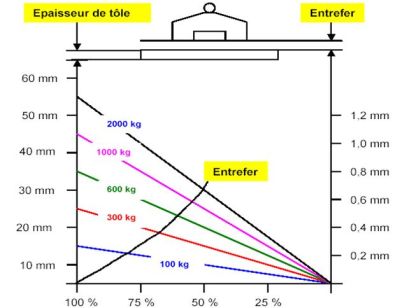
Exemple de méthode d’application
Un aimant de levage présente une capacité nominale théorique de 1 000 kg.
L’objectif est de déterminer la force d’aimantation réellement disponible lors du levage d’une tôle en acier présentant les caractéristiques suivantes :
- Épaisseur : 20 mm
- État de surface : rugosité perceptible
- Composition métallurgique : acier de construction standard
- Entrefer : 1 mm, en raison d’une couche superficielle (peinture, oxydation, dépôt)
À partir des abaques techniques fournis avec l’équipement, les coefficients suivants sont retenus :
- Coefficient d’épaisseur (T) : 0,75
- Coefficient d’état de surface (S) : 0,90
- Coefficient de matériau (M) : 0,80
- Coefficient d’entrefer (G) : 0,70
Calcul de la force d’aimantation
Force d’aimantation=1000×0.75×0.90×0.80×0.70
Force d’aimantation=378kg
Analyse du résultat
La force d’adhérence effective obtenue est de 378 kg.
Cela signifie que :
- la charge à lever ne doit jamais dépasser 378 kg,
- la capacité réelle est réduite d’environ 62 % par rapport à la valeur nominale,
- l’impact principal provient de l’épaisseur limitée, de la rugosité du support et de l’entrefer.
Cas particulier d'une pièce cylindrique
Pour une pièce de forme cylindrique, la surface de contact étant réduite, la force doit être divisée par deux :
378÷2=189 kg
La charge maximale admissible devient donc 189 kg.
Nos aimants de levage les plus populaires sur hellopro.fr
 Aimant de levage TOR PML-A, 2000kg
Aimant de levage TOR PML-A, 2000kg
 Aimant de levage
Aimant de levage